مدل اتمی بور تصویری از چگونگی حرکت الکترون ها به دور هسته ارائه می کند. مدل اتمی بور در تبیین پایداری اتم، طیف گسیلی و جذبی گاز هیدروژن اتمی و محاسبه انرژی یونش اتم هیدروژن با موفقیت همراه بود. همچنین مدل اتمی بور را برای اتم های هیدروژن گونه نیز می توان به کار برد. مدل بور می تواند انرژی یونش و طول موج های طیف خطی اتم های هیدروژن گونه را پیش بینی کند که سازگاری خوبی با نتایج تجربی دارد.
این مدل برای وقتی که بیش از یک الکترون به دور هسته می گردد، به کار نمی رود. زیرا در مدل بور نیروی الکتروستاتیکی که یک الکترون بر الکترون دیگر وارد می کند، به حساب نیامده است. این مدل نمی تواند متفاوت بودن شدت خط های طیف گسیلی را توضیح دهد. برای مثال مدل بور نمی تواند توضیح دهد که چرا شدت خط قرمز با شدت خط آبی در طیف گسیلی هیدروژن با یکدیگر متفاوت است.
مدل اتمی تامسون
جوزف تامسون در سال ۱۸۹۶ میلادی موفق به کشف الکترون و اندازه گیری نسبت بار به جرم آن e/m شد. بنا بر مدل اتمی تامسون اتم کره ای است که بار مثبت به طور همگن در سرتاسر آن گسترده شده و الکترون ها که سهم ناچیزی را در جرم اتم دارند در جاهای خالی آن پراکنده شده اند. در این مدل الکترون ها با بسامدهای معینی حول وضع تعادلشان نوسان میکنند و همین سبب تابش امواج الکترومغناطیسی از اتم میشود. یکی از ناکامی های مدل اتمی تامسون این بود که بسامدهای تابش گسیل شده از اتم با نتایج تجربی سازگار نبود. این مدل را گاهی مدل کیک کشمشی هم میگویند زیرا الکترون ها مانند دانه های کشمش در آن پخش شده اند.

مدل اتمی رادرفورد
آزمایش پراکندگی رادرفورد که در آن ذرات آلفا از یک ورقه نازک طلا پراکنده شده اند را می توانید در شکل زیر مشاهده کنید. تمام وسیله ها در یک اتاقک خلا قرار دارند.
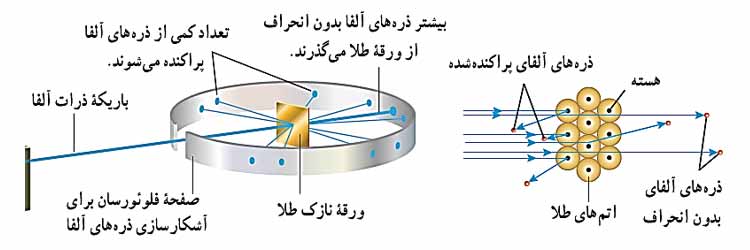
رادرفورد با این آزمایش باریکه ای از ذره های دارای بار مثبت (هسته اتم هلیم که به آن ذره آلفا گفته میشود) را بر سطح ورقه ای نازک از جنس طلا تاباند و مشاهده کرد بعضی از ذرات بدون انحراف و بعضی با انحرف کمتر و بعضی با زاویه بسیار تند منحرف و پراکنده می شدند. رادرفورد نتیجه گرفت که باید هسته ای چگال و دارای بار مثبت در مرکز هر اتم باشد که با مدل اتمی تامسون به طور آشکار مغایرت داشت. به این مدل، مدل اتم هسته ای یا مدل هسته ای اتم می گویند.
مدل اتمی رادرفورد دو مشکل اساسی داشت :
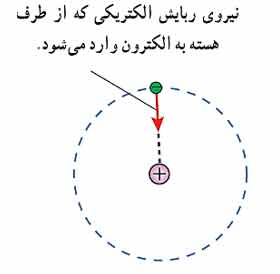
اگر الکترون ها نسبت به هسته ساکن باشند باید تحت تاثیر نیروی ربایشی الکتریکی، الکترون روی هسته سقوط کند و در نتیجه اتم باید ناپایدار باشد چیزی که با واقعیت جور در نمی آید.
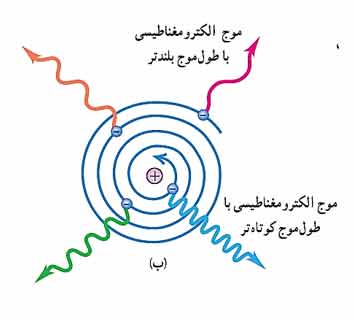
اگر الکترون مانند سیاره های منظومه خورشیدی که دور خورشید میچرخند به دور هسته در گردش باشند باز هم این حرکت پایدار نمی ماند. زیرا حرکت مداری به دور هسته حرکت شتاب دار به طرف مرکز است. در فیزیک کلاسیک حرکت شتابدار الکترون سبب تابش امواج الکترومغناطیسی می شود. با تابش موج الکترومغناطیسی توسط الکترون انرژی آن کاسته شده و باعث میشود که شعاع الکترون به تدریج کوچک تر و بسامد حرکت آن به تدریج بیشتر شود تا الکترون روی هسته سقوط کند. در نتیجه بسامد موج الکترومغناطیسی تابش شده نیز به تدریج زیاد میشود. و این یک طیف پیوسته به ما می دهد در صورتی که در آزمایش ها طیف خطی گسیل شده به صورت گسسته است.
ضعف های مدل اتمی رادرفورد را می توان به صورت زیر خلاصه کرد :
ناتوانی در تبیین پایداری اتم و ناتوانی در توجیه طیف گسسته اتمی
مدل اتمی بور
مدل اتمی بور بر اساس مفروضات زیر بنا نهاده شده است:
۱ – مدارها و انرژی های الکترون ها در هر اتم کوانتیده اند. یعنی فقط مدارها و انرژی های گسسته معینی مجاز هستند.
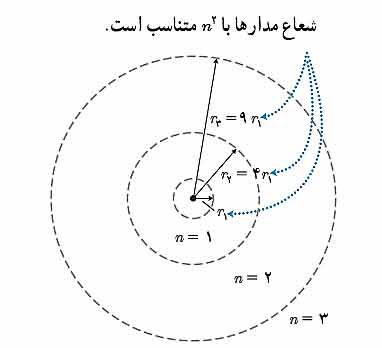
شعاع مدار های الکترون از رابطه زیر بدست می آید.
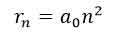
انرژی ترازهای انرژی الکترون در اتم هیدروژن از رابطه زیر بدست می آید.
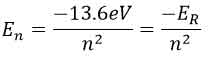
در این روابط n=0,1,2,… اعداد کوانتومی نامیده می شود و a0=5.29×۱۰-۱۱m شعاع بور است.
۲ – وقتی یک الکترون در یکی از مدارهای مجاز است هیچ نوع تابش الکترومغناطیسی گسیل نمیکند. از این رو گفته می شود الکترون در مدار مانا یا حالت مانا قرار دارد.
۳ – الکترون می تواند از یک حالت مانا به حالت مانای دیگر برود. هنگام گذار الکترون از یک حالت مانا با انرژی بیشتر EU به یک حالت مانا با انرژی کمتر EL یک فوتون تابش می شود. در این صورت انرژی فوتون تابش شده برابر اختلاف انرژی بین دو مدار اولیه و مدار نهایی است و رابطه آن به صورت زیر است.
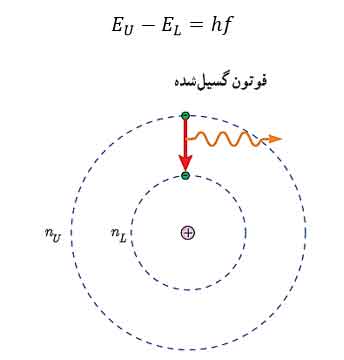
در اتم هیدروژن و در دمای اتاق، الکترون ها اغلب در حالت پایه (n=1) قرار دارند. اگر به آن از طریق گرما یا ایجاد اختلاف پتانسیل الکتریکی انرژی بدهیم، الکترون به تراز های بالاتر که به آن حالت برانگیخته می گوییم می رود و در بازگشت به ترازهای پایین تر امواج الکترومغناطیسی تابش می شود که طول موج این تابش ها با طول موج های بدست آمده از طیف گسسته اتم هیدروژن در آزمایش همخوانی دارد.
اگر بخواهیم الکترون را از اتم خارج کنیم باید الکترون را از تراز n=1 به تراز n=ꚙ ببریم که این مقدار انرژی کمترین انرژی لازم برای خارج کردن الکترون از حالت پایه است و آن را انرژی یونش الکترون نامیده می شود. مقدار پیش بینی شده توسط مدل اتمی بور برای انرژی یونش اتم هیدروژن، توافق بسیار خوبی با مقدار تجربی دارد.
نمودار های تراز انرژی برای الکترون در اتم هیدروژن به صورت شکل زیر است.
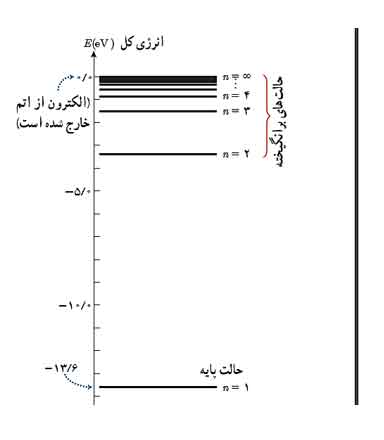
هر چه به ترازهای بالاتر می رویم اختلاف انرژی بین دو تراز متوالی کمتر می شود.
مثال ۱: الکترونی در دومین حالت برانگیخته اتم هیدروژن قرار دارد. الف) انرژی الکترون را در این حالت پیدا کنید. ب) وقتی الکترون از این حالت برانگیخته به حالت پایه جهش می کند نمودار تراز انرژی آن را رسم کنید. پ) طول موج فوتون گسیل شده را حساب کنید.

با استفاده از مفروضات مدل بور براحتی می توان فرمول ریدبرگ را به صورت زیر استخراج کرد.
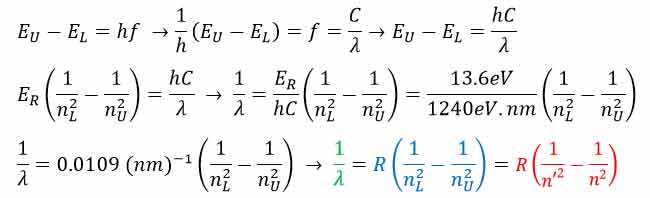
همانطوری که در اثبات بالا مشاهده می کنید که مدل اتمی بور، فرمول ریدبرگ که از طریق داده های آزمایشگاهی بدست آمده بود را تایید کرد.
مثال ۲: در اتم هیدروژن یک الکترون در تراز n=4 قرار دارد. این الکترون به تراز پایه می رود.
الف) طول موج فوتون تابشی تقریبا چند نانومتر است؟R=0/01nm-1
ب) این فوتون در کدام ناحیه از طیف امواج الکترومغناطیسی قرار دارد؟
حل مثال ۲: الف )
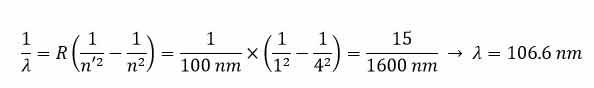
ب) چون این گذار برای رشته لیمان است، در ناحیه فرابنفش قرار می گیرد.
هنگامی که یک الکترون در اتم هیدروژن از تراز n به حالت پایه می رود و همه گذارهای ممکن را در نظر بگیریم، تعداد نوع فوتون هایی که با طول موج متفاوت تابش می شود از رابطه زیر بدست می آید.
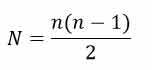
به طور مثال فرض کنید الکترون از تراز ۴ به حالت پایه می رود. همه حالت های ممکن به صورت زیر است:
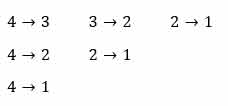
همانطوری که مشاهده میکنید ۶ نوع فوتون تابش می شود که می توانستیم به صورت مستقیم از رابطه زیر بدست آوریم.
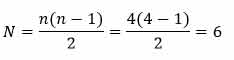
موفقیت ها و نارسایی های مدل اتمی بور
مدل اتمی بور در تبیین پایداری اتم، طیف گسیلی و جذبی گاز هیدروژن اتمی و محاسبه انرژی یونش اتم هیدروژن با موفقیت همراه بود. همچنین مدل اتمی بور را برای اتم های هیدروژن (یون های تک الکترونی) گونه نیز می توان به کار برد. مدل بور می تواند انرژی یونش و طول موج های طیف خطی اتم های هیدروژن گونه را پیش بینی کند که سازگاری خوبی با نتایج تجربی دارد.
این مدل برای ان های چند الکترونی، به کار نمی رود. زیرا در مدل بور نیروی الکتروستاتیکی که یک الکترون بر الکترون دیگر وارد می کند، به حساب نیامده است. این مدل نمی تواند متفاوت بودن شدت خط های طیف گسیلی را توضیح دهد. برای مثال مدل بور نمی تواند توضیح دهد که چرا شدت خط قرمز با شدت خط آبی در طیف گسیلی هیدروژن با یکدیگر متفاوت است.
ویدیو آموزشی
ویدیو آموزشی زیر که در مورد مدل اتمی بور و توجیه طیف خطی هیدروژن اتمی است و توسط استاد مصطفی کبیری آماده شده است، را مشاهده کنید.
مشاهده در یوتیوب | مشاهده در آپارات
تمرین های مدل اتمی بور
تمرین ۱: اگر الکترون اتم هیدروژن از تراز ۴ به تراز ۲ انتقال یابد. الف) این گذار مربوط به جذب است یا گسیل؟ ب) انرژی مربوط به این گذار را بر حسب الکترون ولت به دست آورید. (ER=13.6eV)
تمرین ۲: اتم هیدروژن در حالت برانگیخته n=3 قرار دارد. کوتاه ترین طول موج تابشی آن چند نانومتر است. (R=0.01nm-1)
تمرین ۳: در اتم هیدروژن اگر اختلاف انرژی الکترون بین ترازهای ۱ و۳ برابر ΔE و بین ترازهای ۴ و ۶ برابر ΔE’ باشد. نسبت ΔE/ΔE’ چند است.
تمرین ۴: یک اتم هیدروژن در حالت پایه قرار دارد. بیش ترین طول موج نوری که بتواند این اتم هیدروژن را یونیزه کند، چند نانومتر است؟ (R=0.01nm-1)
دانلود جزوه مطالب بالا و حل تمرین ها
دانلود پاورپوینت تدریس
پاورپوینت در ویدیو آموزشی بالا تدریس شده است.
تعداد اسلاید: ۲۰
فونت: B Koodak
قابل ویرایش می باشد.



5 دیدگاه دربارهٔ «مدل اتمی بور»
قدردان زحمات نویسندگان وکلیه عوامل این سایت وکانال مفیدفیزیکفاهستیم هزاران سپاس برتوضیحات ساده روان دقیق وعلمی
سپاس از لطف شما. محبت شما موجب دلگرمی ماست
بسیار عالی استاد
فقط در بخش تعداد فوتون های ممکن در گذار از لایه n به حالت پایه، در اون مثال ، ۲->1 رو دوبار نوشتید و ۳ به ۱ رو ننوشتید
متشکرم
با تشکر از شما
علت علامت منفی در رابطه
En=-Er/n² چیست؟
چون این انرژی ناشی از نیروی جاذبه هسته بر الکترون است. در نتیجه الکترون در قید هسته است. انرژی الکترون را منفی در نظر می گیریم. اگر مثبت ۱۳.۶ الکترون- ولت انرژی مثبت به الکترون بدهید انرژی آن صفر می شود و این یعنی الکترون در قید هسته نیست.