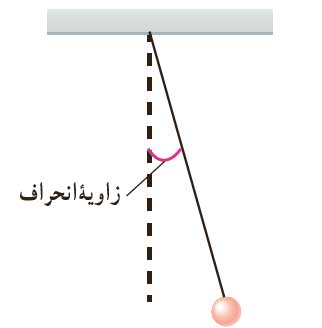
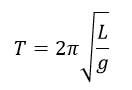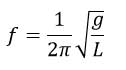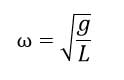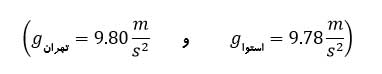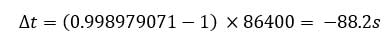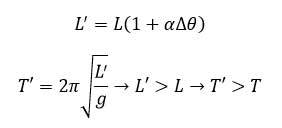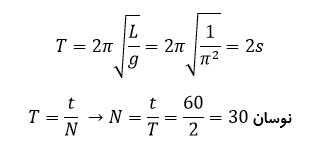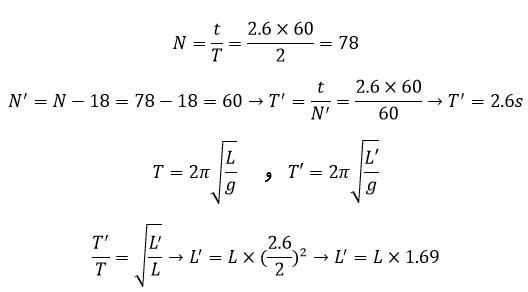آونگ ساده شامل یک وزنه به جرم m که از نخ بدون جرمی (جرم ناچیز) با طول L که از سر دیگر ثابت شده است، آویزان است. اگر زاویه انحراف آونگ از وضع تعادل کوچک باشد، وزنه تقریبا روی یک خط راست حرکت رفت و برگشتی انجام می دهد. اگر از مقاومت هوا هم چشم پوشی کنیم، میتوان حرکت آونگ را حرکت هماهنگ ساده دانست و همان تبدیل انرژی های نوسانگر هماهنگ ساده در اینجا هم اتفاق می افتد.
دوره آونگ ساده
اگر زاویه انحراف آونگ از وضع تعادل کوچک باشد ( باید کمتر از ۱۵ درجه باشد)، مولفه افقی نیروی وزن تقریبا روی خط راست (مثلا محور x ) می افتد و این نیرو موجب می شود وزنه تقریبا روی یک خط راست حرکت رفت و برگشتی انجام دهد.
با صرف نظر از نیروی مقاوم حرکت می توان نتیجه گرفت این حرکت، حرکت هماهنگ ساده است. هم با استفاده از روابط و هم با آزمایش می توان متوجه شد که دوره تناوب آونگ ساده فقط به شتاب گرانشی (g) و طول آونگ (L) بستگی دارد و به صورت زیر است:
این رابطه نشان می دهد که دوره تناوب آونگ ساده، به جرم و دامنه نوسان بستگی ندارد. با توجه به اینکه بسامد عکس دوره تناوب است، خواهیم داشت:
در نتیجه بسامد زاویه ای آونگ ساده را می توان به صورت زیر محاسبه کرد.
مثال هایی از آونگ ساده
مثال۱:
بستگی دوره تناوب آونگ به شتاب گرانشی، روش دقیقی را برای تعیین g به دست می دهد. در این روش با اندازه گیری طول L و دوره تناوب T، می توان g را به دست آورد. ژئوفیزیک دانی با استفاده از یک آونگ ساده به طول ۰٫۱۷۱m که ۷۲ نوسان کامل را در ۶۰ ثانیه انجام می دهد، شتاب g را در مکانی خاص تعیین می کند. وی مقدار g را در این مکان چقدر به دست می آورد؟
پاسخ:
رابطه دوره تناوب را می نویسیم:
مثال ۲:
الف) ساعتی آونگ دار (با آونگ ساده) در تهران تنظیم شده است. اگر این ساعت به منطقه ای در استوا برده شود، عقب می افتد یا جلو؟ مقدار این عقب یا جلو افتادن در یک شبانه روز چقدر است؟
ب) به نظر شما آیا با افزایش دما یک ساعت آونگ دار جلو می افتد یا عقب؟
نحوه کارکرد ساعت آونگ دار را می توانید در شکل زیر مشاهده کنید.

پاسخ:
الف) ابتدا رابطه دوره تناوب آونگ را می نویسیم:
یعنی دوره تناوب ساعت در استوا بیشتر از تهران است . یعنی زمان بیشتری طول می کشد تا آونگ پس از انجام یک نوسان کامل به مکان اولیه خود برگردد این به معنای این است که آونگ کندتر حرکت می کند بنابر این ساعت در استوا عقب می افتد. هر چه دوره تناوب ساعت آونگی بیشتر باشد، زمان کند تر می گذرد. برای به دست آوردن مقدار عقب افتادن در یک شبانه روز به روش زیر عمل می کنیم:
هر شبانه روز برابر ۸۶۴۰۰ ثانیه است.
می توان مقدار جلو یا عقب افتادگی ساعت را به صورت زیر محاسبه کرد. از آنجایی که هر چه دوره تناوب بیشتر باشد، زمان کمتری سپری می شود پس خواهیم داشت :
برای این سوال به صورت زیر حساب می کنیم.
یعنی ساعت به اندازه ۸۸٫۲ ثانیه در هر شبانه روز عقب می افتد.
ب) بر اثر افزایش دما، طول آونگ افزایش پیدا می کند. بنابر این دوره تناوب نیز طبق رابطه زیر افزایش می یابد.
بنابر این زمان تناوب آونگ زیاد می شود یعنی آونگ کندتر حرکت می کند بنابر این ساعت عقب می ماند.
مثال۳:
آونگ ساده ای به طول ۱ متر در محلی که شتاب گرانش زمین در SI برابر g=π۲ است، نوساناتی کم دامنه انجام می دهد. گلوله ی این آونگ در هر دقیقه چند نوسان کامل انجام می دهد؟
پاسخ:
رابطه دوره نوسان آونگ به صورت زیر است:
مثال۴:
دوره نوسان آونگ ساده ای در یک مکان معین برابر ۲ ثانیه است و در مدت ۲٫۶ دقیقه N نوسان کامل انجام می دهد. طول آونگ را چند درصد کاهش یا افزایش دهیم تا در همان مدت و در همان مکان N-18 نوسان کامل انجام دهد؟
پاسخ:
بنابر این طول آونگ باید ۶۹ درصد افزایش یابد.
مثال۵:
دوره تناوب دو آونگ ساده کم دامنه به طول های L1 و L2 به ترتیب برابر با ۳s و ۴s است. دوره تناوب آونگ ساده ای به طول (L1+L2) چند ثانیه است؟ (g=π۲)
پاسخ:
دوره تناوب هر آونگ برابر است با:
ویدیو آموزشی
به ویدیو آموزشی زیر در مورد دوره تناوب آونگ ساده کم دامنه که توسط مصطفی کبیری آماده شده است، توجه کنید.
مشاهده در یوتیوب | مشاهده در آپارات