حرکت نوسانی

حرکت نوسانی :حرکتی است رفت و برگشتی روی پاره‌خط راست، حول نقطه‌ای در وسط پاره‌خط و با شتاب (نیرویی) مناسب و مختلف العلامت با مکان.

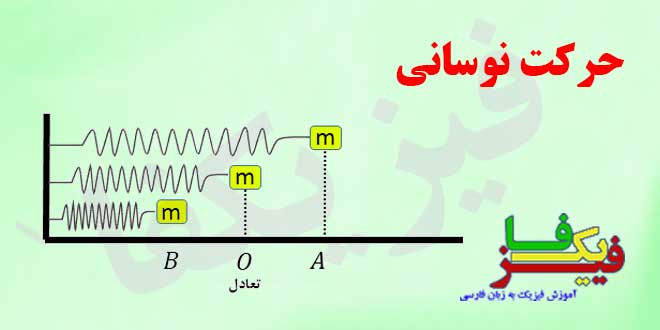
دوره (T): مدت زمانی که طول می کشد تا یک نوسان کامل انجام شود.

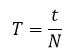
که در آن t کل زمان حرکت و N تعداد نوسان است.

بسامد (f): تعداد نوسان کامل (رفت و برگشت) در ۱ ثانیه

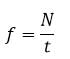
رابطه دوره و بسامد :

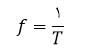
یکای بسامد یک بر ثانیه است که آن را هرتز( Hz ) می نامیم.

بسامد زاویه‌ای : مقدار تغییر زاویه (فاز) بر حسب رادیان بر ۱ ثانیه است.

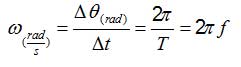
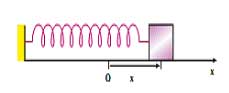
مکان (بعد – وضعیت) x: فاصله نوسان کننده تا مرکز نوسان (نقطه O) می‌باشد.

دامنه (A): بیشترین مکان (بعد بیشینه) را گویند که نصف طول پاره‌خط نوسان است

نکته مهم : دامنه نوسان به مشخصات ظاهری وزنه-فنر یعنی جرم وزنه و ثابت فنر بستگی ندارد. بلکه فقط به این بستگی دارد که وزنه از کجا رها شود. مثلا اگر فنر را به اندازه ۱۰cm نسبت به وضع تعادل بکشیم یا بفشاریم و آن را رها کنیم، دامنه نوسان ۱۰cm می شود.

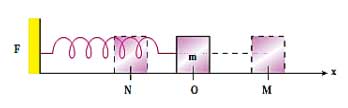
نکات مهم :

۱- با توجه به شکل فوق، در حرکت نوسانی، مقدار x در قسمت OM مثبت ولی در قسمت ON منفی می‌باشد.

۲- در هر قسمت از پاره‌خط NM ،اگر متحرک به سمت راست حرکت کند، v>0  و اگر به سمت چپ حرکت کند، v<0 می‌باشد. مقدار سرعت در نقاط M و N صفر است در حالی که مکان در این نقاط به ترتیب دارای بیشترین مقدار (+A) و کمترین مقدار (-A) است. سرعت هنگام عبور متحرک از نقطه‌ی تعادل O دارای بیشترین مقدار است.

۳- با توجه به رابطه‌ی F=-Kx نحوه‌ی تغییر در اندازه‌ی x و F با هم متناسب است اما علامت‌های متضاد یگدیگر دارند. به عنوان مثال مقدار F در قسمت OM منفی است.

رابطه مکان برحسب زمان یک رابطه سینوسی است و می‌توان آن را از رابطه‌ی نیروی حرکت نوسانی محاسبه نمود:

 

معادله مکان-زمان حرکت نوسانی :

رابطه مکان برحسب زمان یک رابطه سینوسی است و می‌توان آن را از رابطه‌ی نیروی حرکت نوسانی محاسبه نمود:

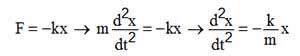
جواب این معادله که مشتق دوم مکان متناسب با منفی مکان است، یک معادله سینوسی و به صورت:

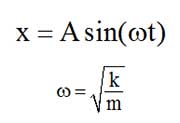
مثال ۱: اگر معادله‌ی مکان-زمان نوسانگر ساده‌ای در SI به صورت زیر باشد، دامنه‌ی حرکت، بسامد زاویه‌ای و بسامد آن به ترتیب چند سانتی‌متر، رادیان بر ثانیه و چند هرتز است؟

حل مثال ۱:

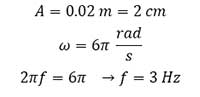
مثال ۲: اگر طول پاره خط نوسان یک نوسانگر وزنه – فنر ۲۰cm باشد و دوره حرکت آن ۰٫۲ ثانیه باشد ، معادله مکان نوسانگر را بنویسید.

حل مثال ۲:

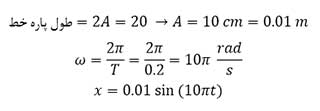
دوره نوسانگر را می توان با استفاده از مشخصات ظاهری وزنه-فنر محاسبه کرد. با توجه به روابط زیر :

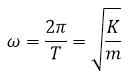
دوره نوسانگر از رابطه زیر بدست می آید :

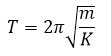
و می توان براحتی نشان داد که بسامد نوسانگر از رابطه زیر بدست می آید :

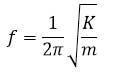
مثال ۳: نوسانگر وزنه-فنر ، روی سطح افقی بدون اصطکاک با دامنه ی  A₁ و بسامد f₁ نوسان می کند. در لحظه ای که نوسانگر در بیشترین فاصله از مرکز نوسان قرار دارد، ۳/۴ جرم وزنه ، کنده شده و جدا می شود. و جرم باقی مانده متصل به همان فنر به نوسان ادامه می دهد. اگر در این حالت بسامد f₂ و دامنه، A₂ باشد. نسبت های زیر را حساب کنید.

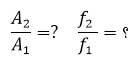
حل مثال ۳:

زمانی که مشخصات نوسانگر عوض می شود وزنه در A₁ قرار دارد. بنابراین خواهیم داشت A₂=A₁ در نتیجه

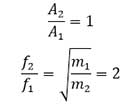
برای مشاهده تمرین های بیشتر جزوه کنکوری نوسان را مطالعه کنید.