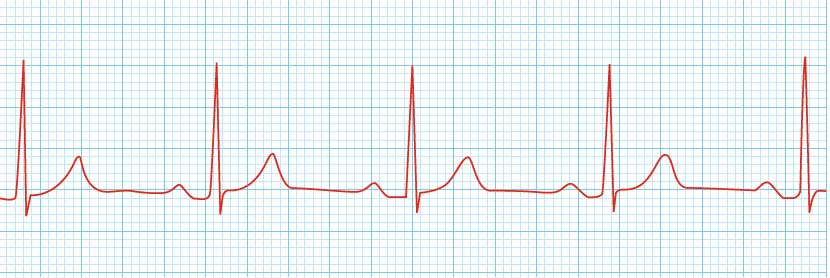
ما در دنیا ، نوسان های زیادی را مشاهده می کنیم از جمله: ضربان قلب، تاب خوردن، نوسان آونگ، نوسان فنر و…. برای درک رفتار نوسان ابتدا باید بدانیم که این نوسان ها دوره ای هستند یا غیر دوره ای. به این معنی که در نوسان دوره ای، نوسان، در هر چرخه، عیناً تکرار می شود. اما در نوسان غیر دوره ای اینطور نیست یعنی ممکن است زمان نوسان یا دامنه نوسان در دور بعدی نوسان تغییر کند. حرکت نوسانگر هماهنگ ساده یکی از مدل هایی است که به ما کمک می کند، تا حرکت نوسانی را راحت تر درک کنیم. برای مثالی از نوسان، نوار قلب یک انسان، نوسانی است دوره ای به صورت شکل زیر.
حرکت هماهنگ ساده
حرکت هماهنگ ساده، یک حرکت رفت و برگشتی روی خط راست است که در آن از نیروهای مقاوم مانند اصطکاک صرف نظر می شود. که در آن هر رفت و برگشت کامل را یک دوره می گویند.
مدت زمان یک چرخه، دوره تناوب حرکت نامیده می شود. که مثلا می توان بین دو نقطه که بیشترین ارتفاع را دارند، در نظر بگیریم.
تعداد نوسان های انجام شده در هرثانیه، بسامد یا فرکانس نوسان نامیده می شود.
یکای بسامد در SI هرتز Hz است که طبق تعریف:
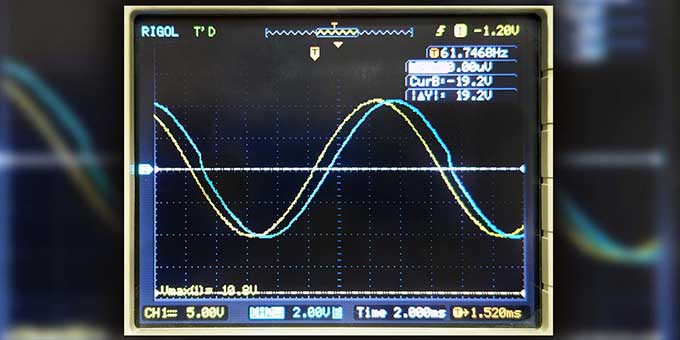
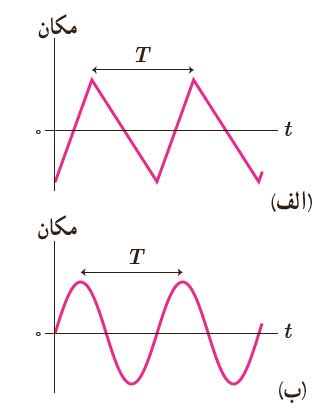
حال نمودار مکان-زمان دو نمونه از نوسان دوره ای را مورد بررسی قرار می دهیم. به شکل زیر نگاه کنید.
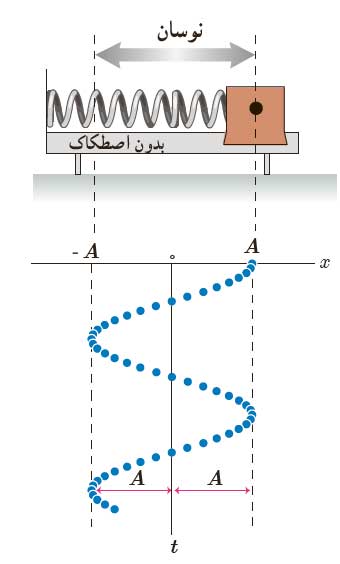
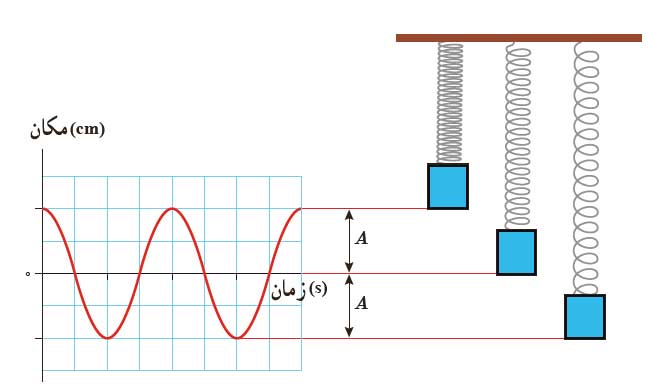
هر دوی این نوسان ها، نوسان های دوره ای هستند. اما به نوسانگری که به شکل سینوسی نوسان می کند، نوسانگر هماهنگ ساده می گویند. همه نوسان های دوره ای را می توان مجموعه ی از نوسان های هماهنگ ساده در نظر گرفت. یک نمونه از حرکت هماهنگ ساده، جسمی است که به سر فنر بسته شده است و نوسان می کند. اگر مکانهای جسم را در زمان های مختلف اندازه بگیریم، مشاهده می کنیم که نمودار مکان زمان این جسم به صورت سینوسی است. در شکل زیر جسم بین x=+A و x=-A نوسان می کند. A دامنه نوسان جسم است. یعنی دورترین فاصله ای که جسم می تواند از نقطه تعادل برود. توجه کنید که دامنه، فاصله بین دو سر مسیر نیست.
معادله حرکت هماهنگ ساده
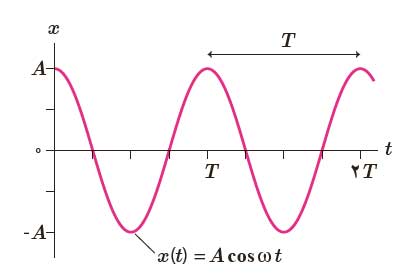
در حرکت نوسانگر هماهنگ ساده، نمودار مکان زمان سینوسی است یعنی مکان را می توان به صورت تابعی سینوسی یا کسینوسی از زمان t نوشت. اگر فرض کنیم در زمان t=0 نوسانگر در دورترین فاصله خود یعنی x=A باشد، مکان نوسانگر را می توان به صورت زیر نوشت:
که در آن ω بسامد زاویه ای نوسانگر است و به صورت زیر تعریف می شود:
یکای بسامد زاویه ای در SI، رادیان بر ثانیه ( rad/s ) است. و عبارتی که داخل کسینوس قرار می گیرد، بر حسب رادیان است.
مطابق شکل بالا وقتی نوسانگر در x=±A باشد، سرعت نوسانگر برابر با صفر است. به این نقطه ها، نقطه بازگشت حرکت می گویند. همچنین وقتی نوسانگر از نقطه تعادل یعنی x=0 بگذرد، سرعت برابر با vmax یا –vmax می شود که علامت آن بستگی به جهت حرکت نوسانگر دارد.
نمودار مکان- زمان حرکت نوسانگر هماهنگ ساده را می توان به صورت زیر رسم کرد.
مثال ۱:
جرمی متصل به یک فنر با بسامد 0.20Hz و دامنه ۳cm به طور هماهنگ ساده در امتداد قائم نوسان می کند. پس از گذشت ۱۰٫۶۶s از رها شدن جرم از بالای نقطه تعادل، جابجایی این جرم نسبت به نقطه تعادل چقدر است؟
پاسخ:
از رابطه زیر برای یافتن جابجایی نسبت به نقطه تعادل استفاده می کنیم:
مثال۲:
ذره ای در حال نوسان هماهنگ ساده با دوره تناوب T است. با فرض اینکه در t=0s ذره در x=+Aباشد، تعیین کنید در هر یک از لحظات زیر، آیا ذره در x=-A ، در x=+A ، یا در x=0 خواهد بود؟
الف) t=2.00T
ب) t=3.5T
پ) t=5.25T
پاسخ:
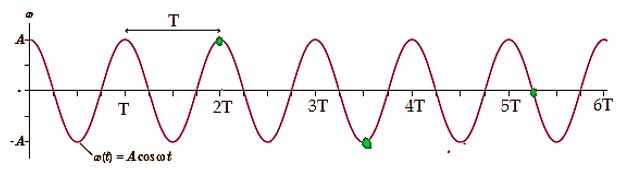
نمودار مکان-زمان نوسانگر را رسم می کنیم و دوره های نوسان را نمایش دادیم.
مطابق شکل بالا،همانطور که با نقاط سبز رنگ نشان داده شده است، در زمان t=2T ، نوسانگر در مکان x=A قرار دارد. در زمان t=3.5T، نوسانگر در مکان x=-A قرار دارد و در زمان t=5.25T ، نوسانگر در مکان x=0 قرار دارد.
مثال۳:
در حرکت هماهنگ ساده، مکان x(t) باید پس از گذشت یک دوره تناوب برابر مقدار اولیه اش شود. یعنی اگر x(t) مکان در زمان دلخواه t باشد، آنگاه نوسانگر باید در زمان t+Tدوباره به همان مکان برگردد و بنابر این Acosωt=Acosω(t+T). بر این اساس نشان دهید ω=۲π/T
پاسخ:
برای اثبات از رابطه داده شده شروع می کنیم.
دوره و بسامد نوسان در سامانه جرم- فنر
آزمایش های متنوع با جرم و فنر نشان می دهد که افزایش جرم m در سیستم جرم-فنر باعث افزایش دوره تناوب T می انجامد. همچنین اگر جرم وزنه ها ثابت باشد اما سختی فنر(k) متفاوت باشد، با افزایش ثابت فنر Tکمتر می شود. بنابر این از رابطه تجربی زیر برای دوره تناوب سیستم جسم و فنر استفاده می شود.
مثال۴:
قطعه ای به جرم ۶۸۰g به فنری با ثابت فنر k=65N/m بسته شده است. قطعه را به اندازه مشخصی از مکان تعادل خود روی یک سطح افقی بدون اصطکاک می کشیم و از حالت سکون رها می کنیم. الف) دوره تناوب و ب) بسامد زاویه ای نوسان چقدر می شود؟
پاسخ:
مثال۵:
یک وزنه ۲۰N را از انتهای یک فنر قائم می آویزیم. فنر ۲۰cm کشیده می شود. سپس این فنر را در حالی که به یک وزنه ۵N متصل است روی میز بدون اصطکاکی به نوسان در می آوریم. دوره تناوب این نوسان چقدر است؟
پاسخ:
در ابتدا باید ثابت فنر را به دست بیاوریم. برای این کار نیروی وارد بر فنر را حساب می کنیم و با نیروی کشسانی فنر برابر قرار می دهیم. به صورت زیر:
حال برای به دست آوردن دوره تناوب نوسان، از رابطه زیر استفاده می کنیم. قبل از آن چون در صورت سوال به ما وزن وزنه را داده است اما در رابطه بالا باید جرم وزنه را وارد کنیم بنابر این باید جرم وزنه را به دست بیاوریم:
مثال ۶:
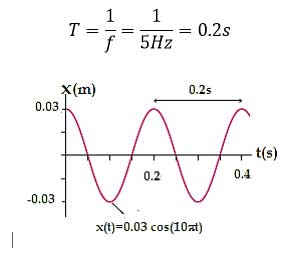
دامنه نوسان یک حرکت هماهنگ ساده ۳×۱۰-۲ متر و بسامد آن ۵Hz است. معادله حرکت این نوسانگر را بنویسید و نمودار مکان-زمان آن را در یک دوره رسم کنید.
پاسخ:
برای رسم نمودار مکان – زمان ابتدا باید رابطه مکان نوسانگر با زمان را به دست بیاوریم که به صورت زیر عمل می کنیم:
دوره تناوب نوسان به صورت زیر است:
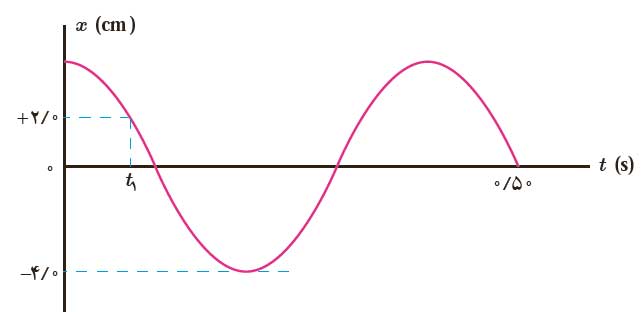
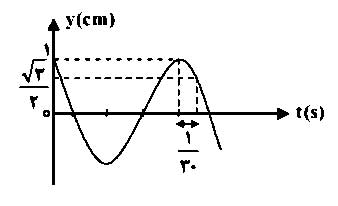
مثال ۷: نمودار مکان-زمان نوسانگری مطابق شکل زیر است:
الف) معادله حرکت این نوسانگر را بنویسید.
ب)مقدار t1 را به دست آورید.
پ)شتاب نوسانگر را در لحظه t1محاسبه کنید.
پاسخ: در حل مساله زمان نشان داده شده در نمودار به جای ۰٫۵ ثانیه، ۵ ثانیه فرض شده است.
الف) از شروع نمودار تا پایان که در زمان 5s نمایش داده شده است، به اندازه یک نوسان کامل به اضافه یک چهارم نوسان طی شده است بنابر این:
ب) در زمان t1 مکان نوسانگر ۲cm است بنابر این با جایگذاری در رابطه به دست آمده در قسمت قبل داریم:
پ) برای به دست آوردن شتاب معادله نیرو را در دو حالت می نویسیم تا معادله شتاب- مکان حرکت هماهنگ ساده بدست آید.
علامت منفی در رابطه بالا از قانون هوک می آید.
در زمان t1 مکان نوسانگر ۲cm است بنابر این با جایگذاری در رابطه بالا داریم:
علامت سرعت و شتاب در ناحیه های مختلف حرکت هماهنگ ساده
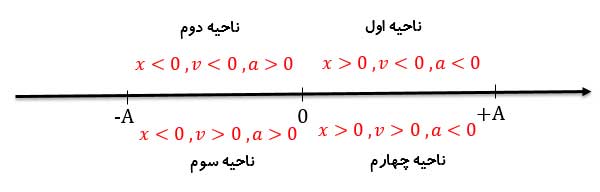
برای تعیین نوع حرکت هماهنگ ساده نیاز داریم علامت های سرعت و شتاب را در مکان های مختلف تعیین کنیم. از اینرو در سامانه جرم- فنر روی خط راست (محور x ) به صورت شکل زیر می توان علامت ها را تعیین کرد. اگر نوسانگر به سمت چپ حرکت کند، علامت سرعت منفی است و اگر به سمت راست حرکت کند، علامت سرعت مثبت است. اگر فنر در حالت کشیده شده (مکانش بعد از نقطه تعادل باشد) باشد، علامت شتاب منفی و اگر فنر در حالت فشرده شده ( مکانش قبل از نقطه تعادل باشد) باشد، علامت شتاب مثبت است.
در نتیجه حرکت در ناحیه های اول و سوم ، تند شونده و در ناحیه های دوم و چهارم ، کند شونده است.
در شکل بالا تعریف ناحیه ها به صورت زیر است:
- ناحیه اول یعنی زمانی که نوسانگر از مثبت A به نقطه تعادل می رود.
- ناحیه دوم یعنی زمانی که نوسانگر از نقطه تعادل به منفی A می رود.
- ناحیه سوم یعنی زمانی که نوسانگر از منفی A به نقطه تعادل می رود.
- ناحیه چهارم یعنی زمانی که نوسانگر از نقطه تعادل به مثبت A می رود.
ویدیو آموزشی از حرکت هماهنگ ساده
ویدیو اول: در این ویدیو که توسط استاد مصطفی کبیری آماده شده است، در مورد نکات و روابط حرکت نوسانی به صورت کامل توضیح داده می شود. و چند مثال در حد امتحانات نهایی برای درک بهتر مطلب حل می شود.
مشاهده در یوتیوب | مشاهده در آپارات
ویدیو دوم: در این ویدیو در مورد استفاده از روش مدت زمان ها در حل برخی از مسائل حرکت نوسانی توضیح داده می شود و در آن چند سوال کنکور سراسری حل می شود.
مشاهده در یوتیوب | مشاهده در آپارات
تمرین ها
تمرین ۱: هرگاه جسمی به جرم m به فنری متصل شود و به نوسان درآید، با دوره تناوب ۲s نوسان می کند. اگر جرم این جسم ۲kg افزایش یابد، دوره تناوب ۳s می شود. مقدار m چقدر است؟
تمرین ۲: جرم خودرویی همراه با سرنشینان آن 1600kg است. این خودرو روی چهار فنر با ثابت ۲٫۰۰×۱۰۴ نیوتون بر متر سوار شده است. دوره تناوب، بسامد و بسامد زاویه ای ارتعاش خودرو وقتی از چاله ای می گذرد چقدر است؟ فرض کنید وزن خودرو به طور یکنواخت روی فنرهای چهارچرخ توزیع شده است.
تمرین ۳: نمودار مکان-زمان نوسانگر ساده ای مطابق شکل مقابل است. دوره آن چند ثانیه است؟
تمرین ۴: جسمی به جرم m به فنری با ثابت k متصل است و با دوره ۰٫۱π ثانیه نوسان می کند. اگر جرم جسم ۱۹۰gکاهش یابد، با دوره ۰٫۰۹π ثانیه نوسان می کند. k چند نیوتون بر سانتی متر است؟
تمرین ۵: نوسانگر وزنه-فنر، روی سطح افقی بدون اصطکاک با دامنه ی A1 و بسامد f1 نوسان می کند. در لحظه ای که نوسانگر در بیشترین فاصله از مرکز نوسان قرار دارد، ۳/۴ وزنه، کنده شده و جدا می شود و جرم باقی مانده ی متصل به همان فنر به نوسان ادامه می دهد. اگر در این حالت بسامد، f2 و دامنه، A2 باشد، نسبت های A2/A1 و f2/f1 را حساب کنید.

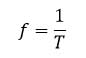
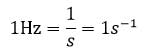
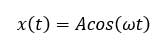
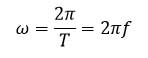

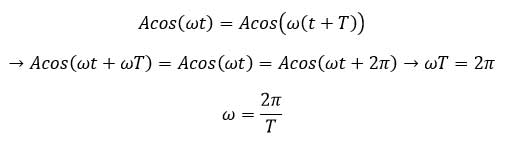
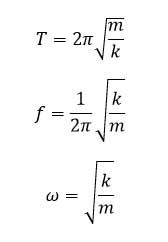

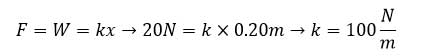
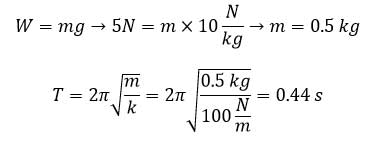
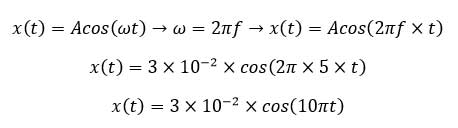
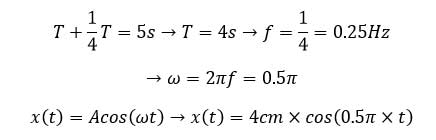
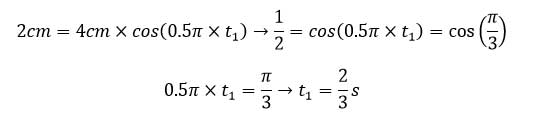
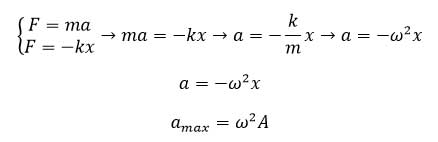
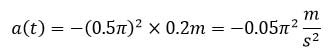

6 دیدگاه دربارهٔ «حرکت هماهنگ ساده»
ممنون از لطف شما
عالیست مطالب و ارایه مطالب.
سپاس از توجه شما. موفق باشید.
با سلام
استاد چرا در قانون هوک از منفی استفاده کردیم لطفاً دلیلش را بگید .
ممنون
در شکل برداری قانون هوک باید علامت منفی قرار داد. چون جهت نیرو و بردار مکان در خرکت هماهنگ ساده در هر لحظه مخالف یکدیگر است. مثلا وقتی فنر کشیده میشه بردار مکان در جهت مثبت محور x است ولی نیرو در خلاف جهت محور x است.
سلام استاد
استاد میشه تو سوال هایی ک مثلا میگه با توجه ب نمودار مکان_ زمان نوسانگری مطابق شکل است شتاب نوسانگر مثلا در لحظه t بدست آورید استاد میشه اینجور سوال هارو هم توضیح بدین
از نمودار مکان- زمان ، مکان نوسانگر را در لحظه t بدست میارید و بعدش تو رابطه شتاب- مکان قرار می دهید. در ویدیوهای حل تست های نوسان و تست کنکورها می توانید حل این دست سوالات را مشاهده کنید.